In 1939, George Bernard Dantzig, a doctorate candidate at the University of California, Berkeley, arrived a few minutes late to Jerzy Neyman’s statistics lecture while there were two homework problems posted on the board. He wrote them down and spent many days figuring out the answers. He was unaware that these were really two well-known statistics theorems that had never been proved before, not just regular exercise problems.
Dantzig subsequently said in an interview that:
A few days later I apologized to Neyman for taking so long to do the homework—the problems seemed to be a little harder than usual. I asked him if he still wanted it. He told me to throw it on his desk. I did so reluctantly because his desk was covered with such a heap of papers that I feared my homework would be lost there forever. About six weeks later, one Sunday morning about eight o’clock, we were awakened by someone banging on our front door. It was Neyman. He rushed in with papers in hand, all excited: “I’ve just written an introduction to one of your papers. Read it so I can send it out right away for publication.” For a minute I had no idea what he was talking about. To make a long story short, the problems on the blackboard that I had solved thinking they were homework were in fact two famous unsolved problems in statistics.
The most renowned statistician in the world at the time, Neyman, was then asked by Dantzig the next year what subject he should choose for his doctoral thesis. Neyman shrugged and said, “Just put your treatments of the two issues in a folder.” He would accept it as a doctoral thesis.
Dantzig’s Early Life
The eldest child of Tobias Dantzig and Anja Ourisson, George Bernard Dantzig was born in Portland, Oregon. The parents had met while attending Henri Poincaré lectures at the Sorbonne in Paris, where they were both students.
They moved to the United States after getting married, where Tobias Dantzig, a native of Lithuania, had to start out by working odd jobs like a road builder and a lumberjack due to language barriers before obtaining a Ph.D. in mathematics from Indiana University; his wife took the master’s degree in French.
The parents thought that their children would have better chances in life if they were given the first names of famous people. Thus, the younger boy was given the first name Henri (after Henri Poincaré) in the hopes that he would one day become a mathematician, while the elder son was given the name George Bernard in the hopes that he would one day become a writer (like George Bernard Shaw).
The father taught mathematics at different institutions, including Johns Hopkins (Baltimore, Maryland), Columbia University (New York), and the University of Maryland, while the mother worked at the Library of Congress in Washington, DC. A book he released in 1930 on the history of the evolution of mathematics, Number – The Language of Science, has been reissued several times (most recently in 2005).
Dantzig continued to struggle with arithmetic in the early grades, but owing to his father’s daily assignment training regimen, particularly in geometry, Dantzig finally received top marks.
George Dantzig started his mathematical studies at the University of Maryland because, despite the fact that both of his parents were employed, the family did not have enough money to finance his studies in physics and mathematics at a prestigious university.
George Dantzig moved to the University of Michigan after receiving a bachelor’s degree, where he went on to complete his graduate studies in 1937. He subsequently accepted a position at the U.S. Bureau of Labor Statistics and participated in research on urban consumers’ purchasing habits after becoming weary of abstract mathematics.
Dantzig Was a Heartfelt Statistician
Dantzig first became interested in statistical concerns and techniques while working in this position. He requested Jerzy Neyman’s permission in 1939 to attend his PhD studies at the University of California, Berkeley (with a “teaching assistantship”). And thus, one day, the event that was described above occurred.
The PhD program was still in progress when the United States joined World War II. Dantzig relocated to Washington, D.C., and accepted a post as the director of the Statistical Control Division at the headquarters of the U.S. Air Force. He discovered that the military’s knowledge of the real inventory of aircraft and equipment was insufficient.
He devised a method to collect the necessary data in detail, particularly to make a thorough contract award, including the need for nuts and bolts.
Dantzig briefly returned to Berkeley after the war, where he eventually received his degree. Not simply for financial reasons but also because he preferred the chances and challenges of working for the Air Force, he declined an offer from the university to continue working there.
Dantzig saw the need to dynamize this rather static model and was motivated by the input-output analysis approach of the Russian-American mathematician Wassily Leontief, who had a position at Harvard University in Cambridge starting in 1931. Additionally, he aimed to improve it to the point where hundreds or even thousands of actions and locations could be recorded and optimized; at the time, this was a fascinating computing hurdle.
Dantzig’s Advancements in Military Planning
While employed by the Pentagon, Dantzig came to the conclusion that many planning choices were based solely on experience rather than objective criteria, yielding less than ideal outcomes. Linear inequalities are often used to characterize the requirements (restrictions), and specifying an objective function establishes the purpose of optimization, such as maximizing profit or decreasing resource consumption.
In English, the planning technique created by Dantzig is known as “linear programming,” where “programming” refers not to programming in the modern meaning of the word but rather to the phrase used in the military for the planning of procedures. The selected linear function modeling is referred to as being “linear.”
A half-plane in two dimensions and a half-space in three dimensions are both defined by a linear inequality. Convex polygons or convex polyhedrons are produced when many inequalities are taken into account; in the n-dimensional case, the corresponding convex structure is known as a “simplex”.
The so-called Simplex Algorithm, which Dantzig created in 1947, is a systematic approach for computing the best answer. Dantzig himself said of it: “The tremendous power of the simplex method is a constant surprise to me.”
The creation of the simplex algorithm, a technique for resolving linear programming problems, is widely regarded as one of Dantzig’s most important accomplishments. The goal of linear programming is to maximize a linear objective function within a set of linear constraints using a mathematical approach. The simplex algorithm has had a significant influence on many fields, including business, economics, and engineering, as a tool for tackling problems in linear programming.
His work on duality in linear programming is a cornerstone of modern optimization theory. To describe the association between a dependent variable and one or more independent variables, he also made significant contributions to the statistical procedure known as linear regression. George Dantzig is called “the father of linear programming” for that.
He Wasn’t Seen Worthy of the Nobel Prize
When Dantzig visited Princeton University to speak with John von Neumann towards the end of the year, the algorithm saw its first refinement. This bright mathematician and computer scientist quickly saw similarities between the methods he and Oskar Morgenstern outlined in their newly released book, “The Theory of Games,” (1944) and the linear optimization approach.
The search techniques have significantly improved over time, notably with the advent of computer use. Although other strategies, such as nonlinear modeling, were also studied, Dantzig’s “linear programming” technique was finally proven to be adequate.
Tjalling C. Koopmans, professor of research in economics at the University of Chicago, realized the value of linear planning from an economic perspective after speaking with Dantzig. His famous theory on the optimal use of exhaustible resources was born out of this. To the surprise of everyone in the field, Dantzig was left unaccomplished when Koopmans received the Nobel Prize in Economics in 1975, together with the Russian mathematician Leonid Vitaliyevich Kantorovich, who had earlier proposed comparable methods in 1939. But it took the West two decades to learn about them. Dantzig, who was always kind to his fellow men, handled this with remarkable perseverance, demonstrating his high degree of expertise.
Dantzig went to the RAND Corporation in Santa Monica in 1952 to continue developing computerized execution of processes after his work with the Air Force. He established the Operations Research Center after accepting a post at Berkeley’s Department of Industrial Engineering in 1960.
When it was first published in 1963 by Princeton University Press, his book Linear Programming and Extensions established the field of linear optimization. Dantzig began working at Stanford in 1966, when he also established the Systems Optimization Lab (SOL). He oversaw a total of 41 PhD students over the course of more than 30 years; all of them had bright futures in academia and the workplace after receiving their degrees from Dantzig.
Dantzig has received multiple honorary degrees and memberships in academies in recognition of his significant scientific accomplishments, including the National Medal of Science and the John von Neumann Theory Prize. The George B. Dantzig Prize is given every three years by the Mathematical Optimization Society (MOS) and the Society for Industrial and Applied Mathematics (SIAM) in recognition of the scientist and his achievements.
His health quickly deteriorated shortly after a celebration of his 90th birthday in 2004; a diabetes condition mixed with cardiovascular issues ultimately caused his death.
The Two Unsolved Homework Problems That George Dantzig Solved
The doctoral student George Bernard Dantzig came late to Jerzy Neyman’s statistics lecture in 1939, when two homework assignments were already written on the board. He put them in writing and spent many days trying to solve them. To him, these seemed like ordinary math exercises, but upon further investigation, he discovered that they were, in fact, proofs of two well-known theorems in statistics that had never been proven previously.
1. “On the Non-Existence of Tests of “Student’s” Hypothesis Having Power Functions Independent of σ”, 1940
In the paper, Dantzig investigates whether or not the power function (i.e., the likelihood of rejecting the null hypothesis) of the statistical test for the “Student’s” hypothesis (commonly known as the t-test) can be designed to be independent of the standard deviation of the population (σ).
The “Student’s” hypothesis is a statistical hypothesis test used to evaluate whether the means of two populations are substantially different from each other; it was named after the statistician William Sealy Gosset, who wrote under the pseudonym “Student.” A common statistical procedure for comparing the means of two samples, the t-test is based on the “Student’s” hypothesis and has extensive use.
Dantzig demonstrated that a power function independent of σ cannot be designed for a statistical test of the “Student’s” hypothesis. He then explained his results and gave evidence for them. The study has received several citations because of its significance for the development of statistical theory.
2. “On the Fundamental Lemma of Neyman and Pearson”, 1951
In 1951, George Dantzig published an article in the Annals of Mathematical Statistics titled “On the Fundamental Lemma of Neyman and Pearson.” As a result of statistical theory, Neyman and Pearson’s fundamental lemma has to do with the power of statistical tests, which Dantzig proves in his article.
Neyman and Pearson’s “fundamental lemma” is a universal conclusion that establishes a connection between the null and alternative hypotheses in a statistical test. If the null hypothesis holds, then the likelihood of detecting a test statistic that is more extreme than a specified value (the critical value) is proportional to the sample size of the test. If the null hypothesis is correct, then the test’s power (the probability of rejecting the null) will be proportional to the test size.
Dantzig provides a demonstration of Neyman and Pearson’s fundamental lemma and examines how this finding has practical consequences for statistical testing in his work. The study has again received a lot of attention for its groundbreaking addition to statistical theory.
George Dantzig, the Real Good Will Hunting
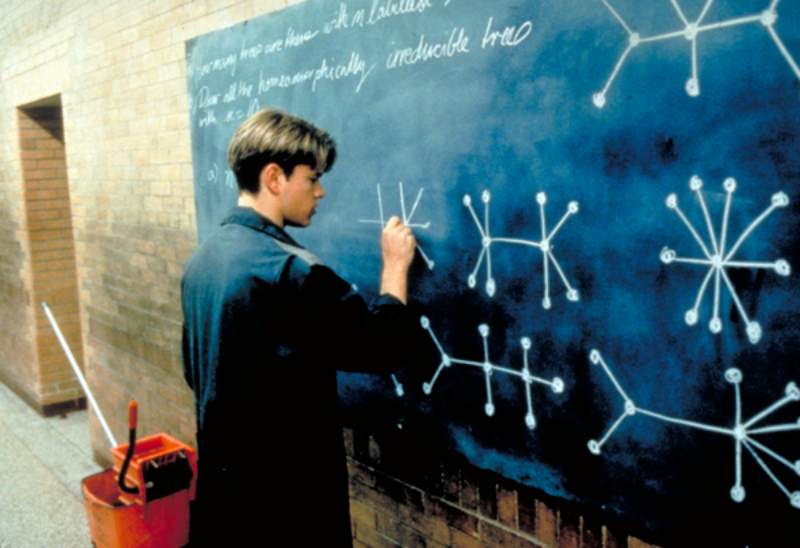
The American drama film “Good Will Hunting,” starring Matt Damon and Robin Williams, was directed by Gus Van Sant and released in 1997. Will Hunting, a young guy from South Boston who is a math prodigy yet works as a janitor at MIT, is the protagonist of this film. An MIT professor sees potential in Will, encourages him to pursue mathematics, and ultimately helps him conquer his own personal issues.
A memorable scene from Good Will Hunting has Matt Damon’s character, a janitor at a university, tackling an almost impossible graph problem on a chalkboard. Certain details were changed for dramatic effect, but the basic tale is based on real events related to George Dantzig. One day, future renowned mathematician George Dantzig was running late to his statistics class when he saw two statistical questions written on the whiteboard and assumed they were homework assignments. Dantzig later casually solved the long-unsolved problems of statistics.
George Dantzig’s Discoveries and Contributions
George Dantzig made important contributions to operations research and mathematical modeling. These are the important discoveries and contributions he made that bear mentioning:
- The simplex algorithm: In particular, Dantzig is lauded for creating the simplex algorithm, a standard technique for resolving linear programming issues. If you have a linear objective function and linear constraints, the simplex method may help you find the best solution.
- The theory of duality in linear programming: Dantzig established a cornerstone notion in optimization theory known as the principle of duality in linear programming. The best solution to a linear programming problem can be found with the help of duality theory, which establishes a link between the original problem and its dual problem.
- Contributions to linear regression: Dantzig’s contributions to the field of linear regression are substantial. Linear regression is a statistical technique for modeling the association between a dependent variable and one or more independent variables, and Dantzig made significant contributions to this area.
- Work on the transportation problem: Dantzig also did important work in the area of transportation problems, a kind of linear programming issue that includes determining the best possible route for resources to take between different points on a map.
When taken as a whole, Dantzig’s contributions to the fields of mathematics and computer science were influential and shaped the manner in which modern corporations and organizations use mathematical modeling to address difficult issues.
References
- Joe Holley (2005). “Obituaries of George Dantzig”.
- Donald J. Albers. (1990). “More Mathematical People: Contemporary Conversations“
- On the Fundamental Lemma of Neyman and Pearson – Projecteuclid.org
- On the Non-Existence of Tests of “Student’s” Hypothesis Having Power Functions Independent of σ – Projecteuclid.org
- Dantzig, George (1940). “On the non-existence of tests of “Student’s” hypothesis having power functions independent of σ“