Hairy Ball Theorem

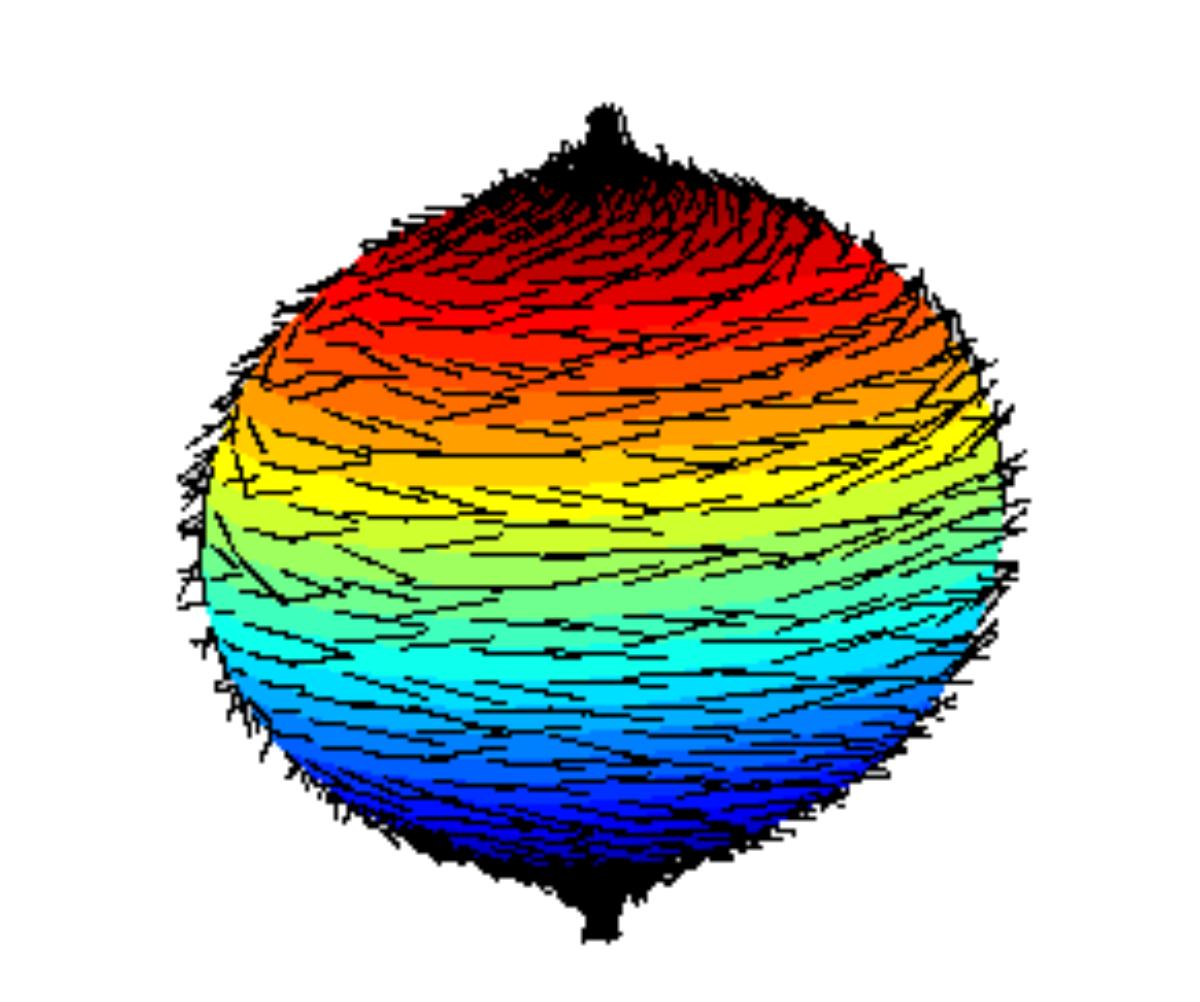
The hairy ball theorem has a variety of applications in the real world outside only combing hair. Nuclear fusion is one example.